gridripper::multipole::Y Class Reference

Class for spherical harmonic functions. More...

#include <Bases.h>

Inheritance diagram for gridripper::multipole::Y:

List of all members.

Public Member Functions

Y (const Y &)

Y (const int L, const int M)

Initialize with the angular momentum quantum numbers.

GComplex_t eval (const GReal_t theta, const GReal_t phi) const

Evaluate it as a function at given coordinates.

Public Attributes

const int l

Index pairs (angular momentum magnitude and direction quantum numbers).

const int m

Detailed Description

Class for spherical harmonic functions.

Spherical harmonic convention ( $\vartheta\in[0,\pi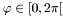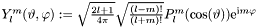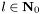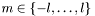]$ , $\varphi\in[0,2\pi[$ ): $Y_{l}^{m}(\vartheta,\varphi):= \sqrt{\frac{2l+1}{4\pi}} \sqrt{\frac{(l-m)!}{(l+m)!}} P_{l}^{m}(\cos(\vartheta)) \mathrm{e}^{\mathrm{i}m\varphi}$ ( $l\in\mathbf{N}_{0}$ , $m\in\{-l,\dots,l\}$ ), where 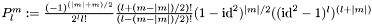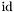$P_{l}^{m}:= \frac{(-1)^{(|m|+m)/2}}{2^{l}l!} \frac{(l+(m-|m|)/2)!}{(l-(m-|m|)/2)!} (1-\mathrm{id}^2)^{|m|/2} ((\mathrm{id}^2-1)^{l})^{(l+|m|)}$ , $\mathrm{id}$ being the identity function of $[-1,1]$ . 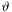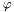We shall denote the identity function of the first projection by $\vartheta$ , and of the second projection by $\varphi$ .

Note: Maple uses the Condon-Shortley phase i.e. 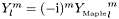$Y_{l}^{m}=(-\mathrm{i})^{m}{Y_{{}_{\mathrm{Maple}}}}_{l}^{m}$ .

Version:: 0.5, 01/31/2007

Since:: GridRipper 0.5

Author:: Andras Laszlo

Constructor & Destructor Documentation

gridripper::multipole::Y::Y	(	const int	L,
		const int	M
	)

Initialize with the angular momentum quantum numbers.

Member Function Documentation

GComplex_t gridripper::multipole::Y::eval	(	const GReal_t	theta,
		const GReal_t	phi
	)			const

Evaluate it as a function at given coordinates.

Reimplemented in gridripper::multipole::Coeff< GComplex_t >.

The documentation for this class was generated from the following file:

gridripper/multipole/Bases.h


Public Member Functions
	Y (const Y &)
	Y (const int L, const int M)
	Initialize with the angular momentum quantum numbers.
GComplex_t	eval (const GReal_t theta, const GReal_t phi) const
	Evaluate it as a function at given coordinates.
Public Attributes
const int	l
	Index pairs (angular momentum magnitude and direction quantum numbers).
const int	m